The sun caused 1,1 °C of the warming since the 17th century

The sun explains 93% of seawater surface temperature variance up to and including 1980s; ozone layer depletion caused more solar radiation on Earth's surface in 1990s, resulting in a persistent spurious relation between CO2 & temperature; afterwards the sun caused further warming in 21st century

May 17, 2020 - Author: Martijn van Mensvoort | English version | Nederlandse versie

In 2020, KNMI researcher Geert Jan van Oldenborgh describes the strong statistical correlation between temperature and CO2 as "an almost perfect connection"¹. However, the link between sun and climate is not understood^2,3. This article describes, based on a total of 40 years around the solar minima over the past 130 years, that the correlation between CO2 and temperature is based on a spurious relation that arises from 2 factors, to wit: a gradual increase in total solar irradiance + an increase in the quantity of solar radiation reaching Earth's surface due to ozone layer depletion.
Seawater surface temperature variance [HadSST3⁴] up to and including the 1980s is explained for 93% by total solar irradiance [LISIRD TSI⁵], after a correction applied to the years around the secondary minima. The 22-year solar cycle provides the physical basis for this correction because the secondary minima occur during the phase when the magnetic poles of the sun have switched positions; while the primary minima arise during the phase with the poles in their original position. The mean values over 3 year periods near TSI minima up to and including the 1980s show a correlation of +0,963 [p=0,000] with sea surface temperature; the correlation between CO2 and sea surface temperature for the same period is only +0,656 [p = 0,000]. A regression analysis shows that the combination of TSI and CO2 does not increase the explained variance for this period compared to the explained variance for the TSI separately; this also applies to when the influence of stratospheric aerosols [AOD⁶] and ENSO [ENS ONI⁷] are also included in the analysis. This implies that the alleged 'footprint' of CO2 is numerically absent in the years around the solar minima through the 1980s.
The relationship between the TSI at the top of the atmosphere and sea surface temperature shows a solar sensitivity of 1,2 °C per W/m2 (involving just the TSI values above 1360 W/m2) for the 3-year average around the minima of the solar cycle; this relation also explains the recent warming between the 3-year periods around the primary solar minima between 1996 and 2017. This connection implies that the sun has been responsible for approximately 1,1 °C of global warming since the Maunder minimum at the end of the 17th century.

During the past 300 years, seawater surface temperature has warmed approximately 1,5 °C; the global temperature rise is 0,15-0,30 °C higher based on a value of about 1,65 °C according the HadCRUT4 and about 1,80 °C according the GISSTEMPv4. 1,1 °C of the warming is attributed to the sun and 0,2 °C to ozone depletion. For the past 130 years the combination of TSI and ozone⁸ explains 96% of the variance in temperature. About 0,2 °C of the sea surface warming remains unexplained. CO2 may have played some role in this, possibly combined with other factors that have had relatively little influence on the long-term trend, such as: ENSO, AOD and aerosols in the lower atmosphere. It is also shown that the same pattern is found in 4 TSI data sets & 4 temperature data sets for the primary minima in in the pre-satellite era; for the satellite era the PMOD-ACRIM controversy is a crucial matter.

In the context of this study, it is important that the IPCC recognizes in AR5 (2013) that the solar cycle phase during minima is both "more stable" and "more relevant" for the long-term trend than it is during maxima.⁹. Also, there is consensus among climate experts that ocean heat content is a "more reliable" indicator of global warming than the atmospheric warming^10-12; logically, therefore the warming of seawater surface temperature is very likely also a more significant indicator. Based on Henry's law, a small part (~15%) of the rise in the CO2 concentration in the atmosphere is the result of sea surface water warming^13-14; it is also known that in the perspective of natural cycles CO2 follows the temperature and not the other way around.

TIP: Figure 10B + figure V show that since the end of the 19th century the solar cycle minima show that seawater surface temperature followed total solar irradiance continuously, with exception to the period between the mid-1980s and mid-1990s.

CONTENTS

• I - CO2 shows a comparable characteristic dynamic in relation to both temperature and total solar irradiance
• II - Sea surface temperature and TSI show a comparable high correlation with CO2 near solar minimum years
• III - After correction, sun shows almost perfect correlation with seawater surface temperature for period including mid-1980s
• IV - Until the 1980s, the sun explains no less than 93% variance in seawater surface temperature
• V - Since the late 19th century, sun and ozone explain 96% of variance in seawater surface temperature
• VI - Since the 17th century, the sun caused ~1.1 °C warming of the seawater surface temperature
• VII - Pre-satellite era: other data sets show the same profile around primary minima
• VIII - Satellite era: ACRIM-PMOD controversy crucial to impact of the sun
• IX - Physical substantiation for impact of sun is conceptually more simple than CO2 hypothesis
• X - Discussion & conclusion

• References

(Data: Excel data file)

I - CO2 shows a comparable characteristic dynamic in relation to both temperature and total solar irradiance

Figure 1 presents a graph made by KNMI researcher Geert Jan van Oldenborgh which describes the statistical relationship between global temperature [GISS] and CO2. The size of the correlation between the two factors is 0,942 [p=0,000; the level of significance is determined using PSPP]. Van Oldenborgh has illustrated the correlation inside the graph with a pink trend line. For the period 1880-1970, the correlation between CO2 and the GISS temperature is considerably lower: 0,616 [p=0,000]. However, these correlations do not unveil the potential relationship between temperature and CO2 in terms of cause and effect. Van Oldenborgh assumes the temperature rise is largely the result of the greenhouse gas CO2 ¹. However, Henry's law describes an inverse relationship between both factors because the concentration of CO2 in the atmosphere depends, among other things, on the temperature of the seawater surface. This implies that the ocean system is less able to absorb CO2 from the atmosphere when the seawater temperature rises. Therefore it is necessary to analyze the dynamics between the two factors in order to determine and understand the nature of the statistical relationship.

In this study the dynamics between temperature and CO2 is studied by means of the most stable phase of the solar cycle: the solar minima. Figure 1 shows the primary and secondary solar minima years accentuated with dark blue and light blue respectively. The values show that up to and including 1985 the temperature during the secondary minima was constantly slightly higher than during the directly surrounding primary minima. At the end of this paragraph is described that the sun shows an opposite phenomenon. Subsequently, a correction will be introduced in paragraph III in order to neutralize the impact of these opposing phenomena.

Figure 1: CO2 shows a strong correlation (r = 0,942 [p=0,000]) with the GISS temperature data set; however, the magnitude of the correlation does not unveil whether there is a causal relationship. For, the period 1880-1970 shows a significantly lower correlation (r = 0,616 [p=0,000]). Based on the LISIRD TSI data set, the primary and secondary solar minimum years are shown in respective with dark blue and light blue color.

The GISS data set (chosen by van Oldenborgh in order to study the relationship between CO2 and temperature) starts in 1880. For this reason this study is focused on the period starting from the year 1880 as well. The analysis is initially focused on 40 years, consisting of the year 1880 plus thirteen 3-year periods surrounding the minima of the 22-year magnetic solar cycle based on the LISIRD TSI data set. The year 1880 is not a solar minimum year, but this year follows immediately after the secondary minimum year 1879. The year 1880 is therefore part included in the analysis, just like all years immediately before and after the 13 minimum years (7 primary minima & 6 secondary minima) according the LISIRD TSI data set.

Just like figure 1, figure 2 describes the relationship between temperature and CO2 as well, but the GISS temperature data set has been replaced by the HadCRUT4 temperature series¹⁵. For the entire period 1880-2018 the correlation between the HadCRUT4 and CO2 is 0,918 [p=0,000], which is only slightly lower than for the GISS temperature data set and CO2 combination. For the 1880-1970 period the HadCRUT4 vs. CO2 correlation is 0,713 [p=0,000], which is an order of magnitude higher compared to the correlation for the same period between the GISS and CO2 (r = 0,616 [p=0,000]).

This shows that the HadCRUT4 describes a more stable correlation with CO2 relative to the GISS; after all, the correlation difference between the two periods is clearly smaller for the HadCRUT4 (difference: 0,918 - 0,713 => 0,205) relative to the GISS (difference: 0,942 - 0,616 => 0,326). Based on this comparison, it can be stated that numerically the instability of the correlation between temperature and CO2 for the GISS is 59% [= (0,326-0,205) / 0,205] higher relative to the HadCRUT4.

Figure 2: CO2 also shows a strong correlation with the HadCRUT4 temperature data set (r = 0,918 [p=0,000].

Figure 2 exhibits that the course of both the primary and secondary minimum years is approximately representative for the course of the entire data set. Both minima series show an oscillating pattern where a magnetic solar cycle featured with a drop in temperature is followed by two successive magnetic solar cycles featured with a temperature rise. In addition to this characteristic dynamic, the primary and secondary minima also show clear differences. In the secondary minima the temperature difference over the double magnetic cycle in the period 1902-1943 represents almost the same temperature difference that is seen for the triple magnetic cycle in the period 1943-2008; the values are in respective: +0,398 °C in 41 years vs. +0,399 °C in 65 years. The primary minima show a temperature increase that is approximately 3x larger during the most recent 2 magnetic cycles in the period 1976-2017 (41 years) compared to during the double magnetic cycle in the period 1912-1954 (42 years). In short, the direction of the movement shows a strong parallel between the primary and secondary minima, but the proportions involving the magnitude of the temperature differences vary strongly between the two minima series.

Figure 3 describes the relationship for the HadSST3 seawater surface temperature series and CO2. For the entire period 1880-2018 the correlation between HadSST3 and CO2 is: 0,878 [p=0,000], which is slightly lower compared to the global temperature series (HadCRUT4 and GISS). For the period 1880-1970 the correlation is: 0,710 [p=0,000], which corresponds fairly accurately to the HadCRUT4 temperature series. This implies that the HadSST3 vs. CO2 combination shows a slightly more stable correlation (difference: 0,878 - 0,710 => 0,168) compared to both global temperature series; the instability of the correlation in the GISS is even up to 94% higher relative to the HadSST3.

Figure 3 also shows for both minima series an oscillation pattern that includes a magnetic solar cycle accompanied with a temperature drop which is followed by two successive magnetic solar cycles featured with a temperature rise. In addition to this characteristic dynamic, the primary and secondary minima also show clear differences here - though these differences are in the perspective of the HadSST3 seawater surface temperature slightly smaller relative to the global HadCRUT4 temperature series.

Figure 3: CO2 also shows a strong correlation with the HadSST3 temperature data set (r = 0,878 [p=0,000]).

The analysis so far shows that prior to 1970 the magnitude of the correlations between CO2 and the various temperature series is clearly much lower than the correlation for the entire period from 1880. In addition, figure 3 shows that the temperature rise of the seawater surface during the 41 years between the secondary minimum years 1902 and 1943 (+0,408 °C) is even significantly larger than the temperature rise during the 43 years between secondary minimum years 1965 and 2008 (+0,368 °C). This indicates that CO2 may not have been largely responsible at all for the temperature rise during both periods.
With regard to the primary minima, it is also striking that figure 3 shows a rate of temperature rise in the 20-year period between 1976 and 1996 that is hardly below the rise during the 21-year period between 1996 and 2017. This provides another indication that CO2 may not have been largely responsible for the temperature rise during these periods.

The characteristic dynamics are not exclusive for just the minimum years of the solar cycle, because the two purple curves in figure 4 clearly show that the characteristic pattern also becomes manifest in the 3-year average values around the minimum.

The two blue curves in the lower part of figure 4 show that the characteristic dynamics also become manifest in the total solar irradiance. After all, the primary minima series of the TSI show an approximately similar pattern: after a fall in the primary TSI minima during a solar cycle, two successive magnetic solar cycles follow with an increase of TSI. Additionally, one can notice here that the TSI secondary minima show a deviation in the pattern during the transition from the period 1901-1903 to the period 1921-1923 with a (small) decrease, while the temperature shows an increase.

Figure 4: The total solar irradiance (TSI) shows for the 3-year average values around the minima almost the same characteristic pattern that is present in the temperature data. Only the secondary minima show a difference in direction at the first temperature and TSI transition.

A striking difference between sea surface water temperature and TSI is that only in the latter perspective the curve with the secondary values is largely found below the primary values. In the period up to and including the 1980s the curve of the secondary temperature values is largely above the primary temperature values. This points towards the possibility that the content of the solar radiation during primary and secondary solar minima differs substantially from each other, so that lower secondary TSI may be associated with higher secondary temperatures. This phenomenon shows a clear parallel with the Gnevyshev-Ohl rule¹⁶, which is associated with solar proton events and structural changes in the sun's magnetic field¹⁷ - this field determines the amount of cosmic rays that can reach Earth. According simple logics, the magnetic cycle of the sun therefore also plays a role in the composition of the Earth's atmosphere, which has an influence on the climate¹⁸.

Figure 4 shows for both perspectives a trend channel in the form of yellow zones based on the first 3 primary minima (which represent the most stable phase of the solar cycle). After all, only at the primary minima the poles of the sun are in the original position; while the poles have switched positions when the secondary minima become manifest. Only the average TSI values of the last two primary periods (1984-86 and 2016-18) are inside the corresponding trend channel, while for the seawater surface temperature the average values of the last two primary periods are found well above the trend channel. A confirmation for this represents the relatively large distance between the temperature and the TSI during these periods. A major difference between the temperature and the TSI becomes manifest at the transition between the primary years 1975-77 and 1995-97: only the temperature has clearly increased during this transition, while the TSI shows a minimal increase only.

Figure 4 also shows that the distance between temperature and TSI remains stable up to and including the 1984-86 period. This suggests that the warming that becomes manifest on top of the impact of the gradually increased activity of the sun did not clearly start yet during the mid-1980s. Also, one should notice here that temperature and TSI both have a significantly lower value for the secondary 1984-86 period compared to the secondary 1942-44 period (both perspectives also show values for the 1964-66 period which are slightly lower than the 1984-86 period).

Ozone layer depletion + the emergence of the seasonally related hole in the ozone layer at the South Pole have become manifest from the year 1979. Because the ozone layer is responsible for blocking ultraviolet [UV] solar radiation - a large part of the high-frequency part of solar irradiance is therefore being prevented from reaching the Earth's surface - this implicates that ozone depletion has contributed to the warming of the lower atmosphere. Figure SPM.5 in IPCC AR5 confirms that ozone [O3] can be held responsible for a significant contribution to the warming of the atmosphere. For, O₃ plays a role in the radiative forcing of no less than 5 anthropogenic emitters. 4 Out of 5 factors provide a net contribution to the increase in radiative forcing¹⁹; the largest contribution is associated with methane [CH4].

Consistent with figure 4, paragraph II will demonstrate that near the solar minimum years the correlation between CO2 and the seawater surface temperature does not differ much from the correlation between CO2 and the TSI. Subsequently, paragraph III and paragraph IV present two different analysis techniques which present results showing that the combination of sun and ozone largely explains the gradual warming during the past 130 years.

II - Sea surface temperature and TSI show a comparable high correlation with CO2 near solar minimum years

The first paragraph presented the dynamics for the minimum years; in this paragraph the perspective of the analysis is made larger by including the years immediately before and after the minima. Figure 5 describes the correlation between seawater surface temperature and CO2 (for the period starting from 1880 at the primary minimum years + the immediately surrounding years), which shows almost the same size for the correlation between seawater surface temperature and TSI. These correlations relate to a total of 21 years around the primary minima; the correlation value is, respectively, for seawater surface temperature & CO2: 0,916 [p=0,000] and for seawater surface temperature & TSI: 0,902 [p=0,000].

The period up to and including the late 1970s shows in figure 5 for the correlation between TSI & CO2 a value of 0,813 [p=0,000], which is not much smaller than the correlation for the entire period. On the other hand, the correlation between temperature & CO2 shows a value of 0,544 [p=0,018], which is considerably lower than the correlation for the entire period.

Figure 5: In the 21 years around the primary solar minima for the entire period starting from the year 1880, seawater surface temperature [HadSST3] vs. CO2 (r = 0,916 [p=0,000]) shows a correlation of comparable magnitude relative to the correlation for seawater surface temperature vs. TSI [LISIRD] (r = 0,902 [p=0,000]). The period up to and including the 1970s exhibits that seawater surface temperature only shows a stable correlation with TSI as it is comparable with the correlation for the entire period; while for CO2 the correlation at the primary minima for the period up to and including the 1970s is much lower.

Subsequently, figure 6 shows for the secondary years + the directly surrounding years that the correlation between seawater surface temperature and CO2 in the period starting from 1880 shows exactly the same value as seen for the correlation between seawater surface temperature and TSI. These correlations relate to a total of 19 years and both have the value 0,832 [p=0,000].

For the period up to and including the 1970s, the correlation for TSI and sea surface temperatur shows a value of 0,808 [p=0,000] whic is also not much lower compared to the secondary minima covering the entire period. While the correlation for CO2 and sea surface temperature show with a value of 0,633 [p=0,010] a considerably lower value compared to the entire period. In short, the primary and secondary years separately show roughly the same overall picture: a stable correlation is found only for the combination of the seawater surface temperature and TSI.

Figure 6: The 19 years near the secondary solar minima exhibit for the entire period starting from 1880 that seawater surface temperature [HadSST3] and CO2 produce a correlation (0,832 [p=0,000]) that is also found for seawater surface temperature and TSI. The period up to and including the 1970s exhibits that seawater surface temperature only shows a stable correlation in relation to TSI; for CO2 the correlation during this period at the secondary minima is significantly lower.

Figure 7 shows for the primary and secondary years combined that the overall picture hardly changes in a comparison to the primary and secondary years separately. For the 40 years spread over the entire period the correlation between the seawater surface temperature and CO2 shows a value of 0,885 [p=0,000], which deviates only slightly from the average correlation for the primary and secondary years separately. The correlation for sea surface temperature and TSI is approximately of the same size, even though this correlation is slightly smaller with a value of 0,841 [p=0,000].

For the period up to and including the late 1970s, the correlation value for CO2 (r = 0,547 [p=0,001]) involving the combination of primary and secondary minima is again much lower than for the TSI (r = 0,728 [p=0,000]) is.

Figure 7: The 40 years around the solar minima for the period starting from the year 1880 show for seawater surface temperature [HadSST3] a correlation of the same magnitude with respect to CO2 (r = 0,885 [p=0,000]) and TSI (r = 0,841 [p=0,000]).

Figures 5 to 7 show that for the years near the solar cycle minima the high correlation between seawater surface temperature and CO2 is by no means unique. Both the primary minima & secondary minima and the combination of both minima series, the correlation between seawater surface temperature and TSI consistently shows a magnitude of comparable size. Moreover, the values in the 100-year period between 1880 and the late 1970s show that the correlations between temperature and sun is clearly more stable than the correlations with CO2 involved.

Important as well, only the correlation between TSI and the sea surface temperature does not include any uncertainty in terms of cause and effect. One can only speculate about the possibility that the correlations involved are based on a spurious connection - though in terms of the fundamentals there is no specific reason to suspect that this is actually the case, because after all: the sun is without any doubt the driving force behind the climate system.
In contrast, the correlation between CO2 and seawater surface temperature is by no means based on an unambiguous mechanism in terms of cause and effect. For, on the one hand, CO2 as a greenhouse gas has the potential to contribute to a temperature rise itself. However, on the other hand, Henry's law shows that an increase in ocean temperature can lead to a higher value of CO2 in the atmosphere. So, there is a clear inconsistency involved. Actually, in 2020 the greenhouse theory is still mainly based on 'consensus', while this theory can by no means be considered 'proven' based on empirical data. In 2015 the very first empirical evidence was claimed demonstrating that CO2 has some influence - ~10% of the trend - on the 'back radiation' of long-wave radiation (= infrared radiation) from the atmosphere²⁰. Another significant side note involves the fact that it is known from the natural cycles that CO2 follows temperature and not the other way around. This latter point applies to short and long term cycles, such as: the diurnal cycle ²¹, the seasonal cycle ²¹ and the ice age cycle ²².

Finally, figure 7 shows another significant detail. Only the TSI shows for the period up to and including the 1970s a clearly lower correlation after the two minima series have been combined (r = 0,728 [p=0,000]); while figures 5 & 6 show correlations that are much higher for both the primary minima (r = 0,813 [p=0,000]) and the secondary minima (r = 0,808 [p=0,000]). The following paragraph will show that this phenomenon can be neutralized by means of a correction (aimed at the secondary minima); after applying the correction, the average values over 3 years around the minima exhibit for seawater surface temperature & TSI an almost perfect correlation for the period up to and including the 1980s.

III - After correction, sun shows almost perfect correlation with seawater surface temperature for period including mid-1980s

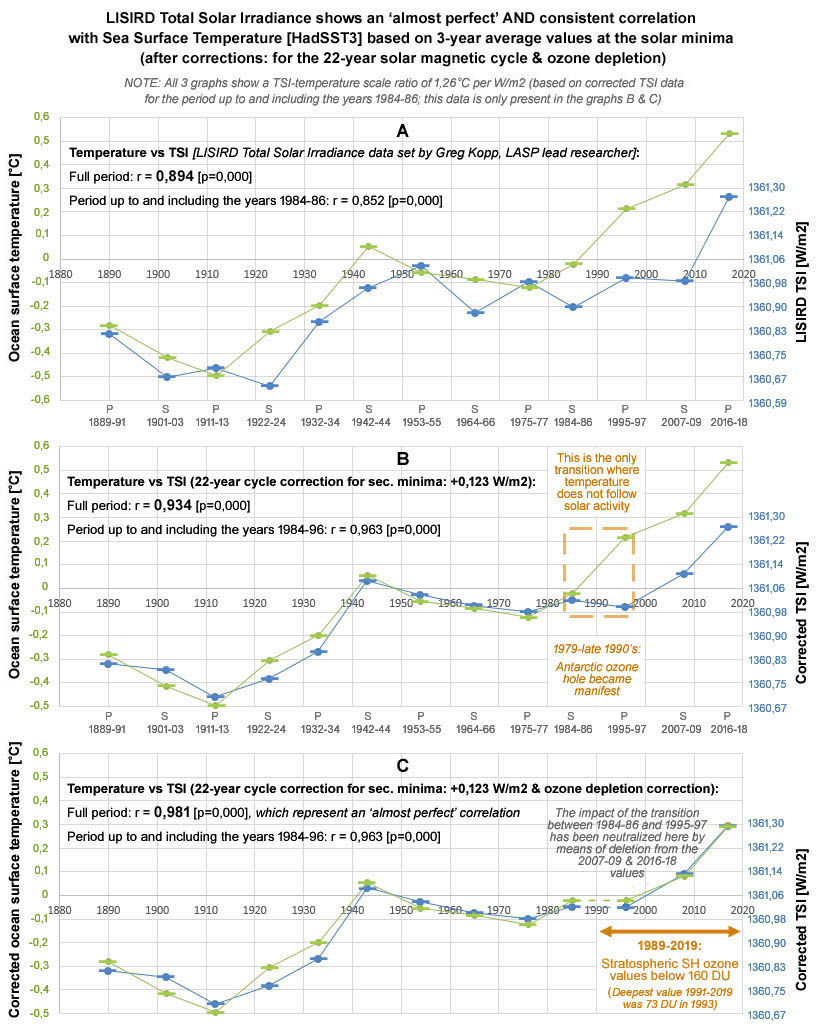
In the first paragraph figure 4 shows a structural phenomenon related to the 22-year magnetic solar cycle; it shows for the primary and secondary minima a parallel with the Gnevyshev-Ohl rule (though this rule only involves the sunspots number at maxima). The secondary TSI values are structurally below the nearest primary TSI values; however, temperature shows a tendency in the opposite direction. Subsequently, figure 7 in the second paragraph points out that after merging primary and secondary minima a considerable part of the correlation between sea surface temperature and TSI is lost - this effect is particularly visible in the period up to and including the 1970s.

Curiously, the impact of the correlation loss can be reversed via a simple correction aimed at the secondary minima (where TSI values have been increased with a value of: +0,123 W/m2). Figure 8 describes the result after applying the correction; the correction only applies to the panel on the right side of figure 7, the panel on the left side of figure 7 has remained unchanged in figure 8. After applying the correction, the correlation between seawater surface temperature and TSI for the combined minima series in the period up to and including the 1970s rises to a value of 0.813 [p = 0.000]. The new correlation corresponds exactly to the correlation value for the primary minima (r = 0,813 [p=0,000]); also, the deviation from the correlation value for the secondary minima (r = 0,808 [p=0,000]) is just small. Moreover, after applying the correction the correlation for the entire periode (r = 0,874 [p=0,000]) has also increased slightly compared to the value without the correction (note: figure 7 shows for the primary and secondary minima combined before the correction for the entire period a value of 0,841 [p=0,000]).

Figure 8: After increasing the TSI secondary minima with a value of 0,123 W/m2, the correlation between seawater surface temperature and TSI for the period up to and including the 1970s becomes for the two minima series combined restored to a value of 0,813 [p=0,000]; the corrected correlation value exactly matches the value at the primary minima (r = 0,813 [p=0,000]) and the deviation is also very small compared to the value for the secondary minima only (r = 0,808 [p=0,000]).

Figure 8 describes for the temperature impact of the sun during the most recent period starting from the 1990s, an average value of 1,14 °C per W/m2 around the minima. This value corresponds approximately to the average value of 1,08 °C per W/m2 found for the years around the minima in the period 1880-1980s. In addition, various intermediate periods show values of the same magnitude.
Also, the correlations between temperature and sun show in a comparison between the period up to the 1970s and the entire period a very high level of consistency (difference: 0,874 - 0,813 => 0,061). While the correlations between temperature and CO2 show in a comparison focused on both periods a low level of consistency (difference: 0,885 - 0,547 => 0,338).

Following figure 8, the result after the correction based on the 3-year average values around the minima is shown in figure 9. The left panel of figure 9 shows for CO2 a likewise characteristic oscillating dynamic that has also been described in section I for the individual primary and secondary minima separately. This implicates that the characteristic dynamic is also present in the perspective of the 3-year average at the minima.
In the right panel of figure 9 the sun shows an almost perfect correlation with temperature over the entire period, with exception to the transition between the minima in the 1980s and 1990s. The period from 1979 to the mid-1990s became known as the period in which the ozone problem became manifest. In 1991 the ozone concentration first reached the level of 100 DU and a few years later it bottomed out in 1994; from the late 1990s ozone levels have subsequently stabilized²³.

Figure 9: After applying the correction (targeted at the secondary minima with a value of: +0,123 W/m2), the 3-year TSI average at the solar minima shows an almost perfect correlation with the sea surface temperature over almost the entire period. Only the transition between the minima in the 1980s and 1990s shows an inconsistent course between both factors. This inconsistency coincides with the time span in which the season-related hole in the ozone layer at the South Pole became manifest. The most recent trough phases of the multi-decadal cycle are also shown; the intermediate period is likely representative for the short phase of the Gleisberg cycle.

Figure 9 shows a remarkable picture, because: for the period up to and including the mid-1970s, the period up to and including the 1980s, as well as the entire period, the combination of seawater surface temperature and total solar irradiance shows an almost perfect correlation. In addition, it also shows that based on the 3-year average at the minima the correlations between temperature and CO2 (left panel in figure 9) are consistently lower for all three periods than the correlations between temperature and total solar irradiance (right panel in figure 9). Only the correlations involving the sun show a stable development for all three periods. This shows that the sun represents an underlying explanatory factor for the emergence of the strong statistical correlation between CO2 and temperature. In short, the stable consistent correlations between sun and temperature show that the sun has been largely responsible for the temperature rise according simple logics (in paragraph VI the possibility is examined whether CO2 also plays a role in this).

Figure 10 shows the impact of the correction based on the 22-year solar cycle (via the secondary TSI minima) in a more direct format based on the 3-year average values. Figures 10A and 10B describe the perspective without and with the correction; figure 10C describes the impact of a neutralization of the (inconsistent) transition between the minimum periods in the 1980s and 1990s.
Figure 10 shows in just 2 steps how a consistent and 'almost perfect correlation' is found for the 3-year periods at the minima with regard to the combination of the sun and the temperature for the entire period. The relationship between the scales for temperature and total solar irradiance has been determined by means of a regression analysis based on the 3-year values for the minima in the period up to and including the 1980s (note: this involves data over a period of almost 100 years starting from the 3-year period around the primary minimum in 1890). This ratio of the scales corresponds to a solar sensitivity of 1,26 C per W/m2 based on the TSI at the top of the atmosphere (section IX provides a numerical description for the perspective of Earth's surface + the necessity for a physics enhancing mechanism for the influence of the sun).

Figure 10: After corrections for the 22-year magnetic solar cycle and the ozone problem, total solar irradiance shows a consistent and 'almost perfect correlation' with seawater surface temperature. Figure 10A shows the 3-year mean minima values for the LISIRD TSI and HadSST3 seawater surface temperature; in figure 10B the secondary [S] TSI values have been raised with a value of +0,123 W/m2 (= a correction due to the exchange of the magnetic poles in the perspective of the 22-year solar cycle); finally, a second correction has been applied in figure 10C (in connection with the ozone problem), whereby the impact of the transition between the periods 1984-86 and 1995-97 has been neutralized for the last 3 minima periods. NOTE: The multiplication factor 1,26 °C per W/m2 only applies to the part of the TSI value above 1360 W/m2.

Figure 10 shows that next to the part of the global warming that has arisen due to the ozone problem (impact: 0,266 °C), the remainder (impact: 0,548 °C) of the total global warming (impact: 0,814 °C) is explained by the sun - after applying the correction aimed at the secondary minima [S]. Because both figure 10A and figure 10B describe that the sun has caused a warming of 0.581 °C in the perspective of the primary minima [P] and the combination of figures 10B & 10C show indicatively that the sun combined with the ozone problem caused a warming at the order of 0.847 °C (= 0.581 °C + 0.266 °C). Striking about figure 10C is that the deviation between temperature and TSI is only relatively large for the first 5 minima periods (1890s to 1930s), while the most recent 7 minima periods (1940s to 2010s) show relative small differences.

However, figure 10 does not yet take into account the possibility that the sun combined with other factors might possible explain a larger part of the variance. The following paragraphs aim to investigate this further on the basis of 5 climatic components: TSI, ozone, CO2, AOD & ENSO.

IV - Until the 1980s, the sun explains no less than 93% variance in seawater surface temperature

An analysis involving five climatologic components shows that the adjusted TSI (after the correction aimed at the secondary minima) leaves little room for the influence of other factors. The overview below shows for the period up to and including the 1980s that in the perspective of 3-year minima, no less than 93% of variance in seawater surface temperature is explained by the adjusted TSI.

• TSI [LISIRD] with adjustment (+0,123 W/m2) of secondary values:
- Full period: R = 0,93; R-square = 0,87 (explained variance = 87%); p=0,000
- Period up to and including '80s: R = 0,96; R-square = 0,93 (explained variance = 93%); p=0,000

• TSI [LISIRD] without adjustment of secondary values:
- Full period: R = 0,89; R-square = 0,80 (explained variance = 80%); p=0,000
- Period up to and including '80s: R = 0,85; R-square = 0,72 (explained variance = 72%); p=0,002

• CO2:
- Full period: R = 0,92; R-square = 0,84 (explained variance = 84%); p=0,000
- Period up to and including '80s: R = 0,66; R-square = 0,44 (explained variance = 44%); p=0,037

• Ozone (size hole in ozone layer):
- Full period: R = 0,82; R-square = 0,67 (explained variance = 67%); p=0,001
- Period up to and including '80s: (no analysis possible because all values are zero for this period)

• AOD [NASA]:
- Full period: R = 0,30; R-square = 0,09 (explained variance = 9%); p=0,323
- Period up to and including '80s: R = 0,01; R-square = 0,00 (explained variance = 0%); p=0,986

• ENSO [ENS ONI with 6 months impact delay]:
- Full period: R = 0,11; R-square = 0,01 (explained variance = 1%); p=0,712
- Period up to and including '80s: R = 0,39; R-square = 0,15 (explained variance = 15%); p=0,271

This overview shows for the individual components that only the TSI explains more than 50% of variance in seawater surface temperature up to and including the 1980s; this applies to the TSI both with and without the correction.

Also, with a single regression analysis [executed with the statistics program PSPP] is investigated whether CO2 combined with the corrected TSI can contribute to the explained variance for the period up to and including the minimum period 1984-86. This is not the case because the explained variance based on the corrected TSI only is 93%, while the corrected TSI combined with CO2 results in an explained variance of just 91% (based on 'adjusted R-squared' values); moreover, the contribution of CO2 is also not significant here.
Investigated as well is to what extent AOD and/or ENSO contributes to the explained variance, with and without CO2; this is not the case for the individual factors and neither for all possible combinations with these factors involved. This implies that for the period up to and including the 1980s the other factors do not generate any significant added value compared to the impact of the adjusted TSI.

Also, the combination of TSI and CO2 provides no added value for the 72% explained variance found based on the uncorrected TSI. For, a regression analysis shows that the explained variance based on the adjusted R-square decreases to 70% for the combination involving the uncorrected TSI and CO2. Here as well only the TSI component makes a significant contribution to the combination. Combinations with AOD and/or ENSO for the period up to and including the 1980s do not generate any added value here in terms of the explained variance (based on 'adjusted R-squared' values).

V - Since the late 19th century, sun and ozone explain 96% of variance in seawater surface temperature

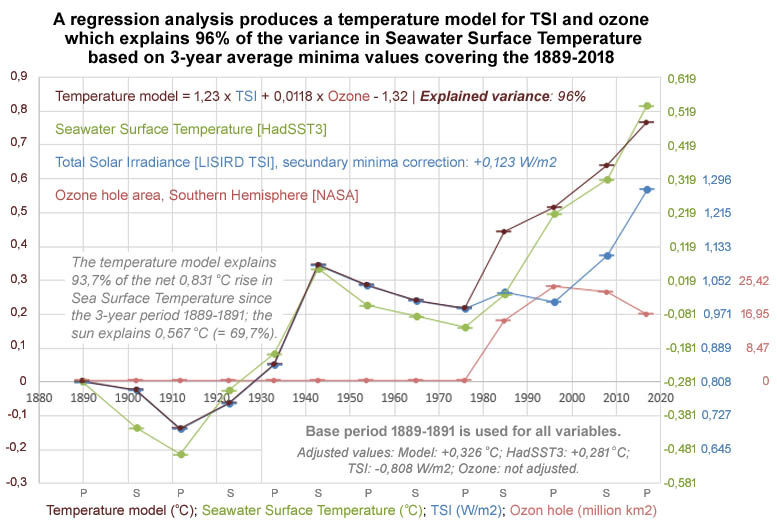
Paragraph III has been used to describe a first indicative estimate for the impact of the adjusted TSI combined with ozone; however, implicit it was assumed that the impact of the ozone problem has remained stable since the 1990s. Earlier, the February article made use of the size of the seasonal hole in the ozone layer near Antarctica⁸ in order to study the influence of the weakened ozone layer.

A regression analysis based on 3-year average values shows that the adjusted TSI combined with ozone layer hole size produces an adjusted R-squared value of 0,96; this implies that 96% of sea surface temperature variance in the perspective near the minima is explained by the combination of sun and ozone for the entire period from the 3-year period around the minimum year 1890. In addition, both components make a highly significant contribution to this result (with p-value: 0,000). Without the correction aimed at the minima, the combination explains 91% of the variance in seawater surface temperature for the entire period in the years near the minima.

Also, it has been investigated to what extent the components CO2, AOD and ENSO generate added value for the entire period in terms of the explained variance within the perspective of the 3-year average values at the minima. This is by no means the case and this also applies to both the TSI values without and with the correction aimed at the secondary minima.

Figure V: A regression analysis produces a temperature model for the TSI and ozone that explains 96% of the variance in surface water temperature based on the 3-year mean around the minima. The temperature model explains 93.7% of the 0,831 °C warming that has arisen since the period 1889-1891; the sun explains 0,567 °C (= 69,7%) of this warming. This implies that the warming contribution of ozone is 0,195 °C (rounded: 0,2 °C). NOTE: The multiplication factor of 1,23 °C per W/m2 only applies to the part of the TSI value above 1360 W/m2; figure V describes only the TSI part above 1360 W/m2.

VI - Since the 17th century, the sun caused ~1.1 °C warming of the seawater surface temperature

In paragraph III figure 10 describes (after applying the correction aimed at the secondary minima) a solar sensitivity of 1,26 C per W/m2; this value applies to the TSI value above 1360 W/m2 and has been established with a regression analysis. In addition, figure 10C shows that after an additional correction focused on the transition between the minima periods 1984-86 and 1995-97, the sun shows an indicative "near-perfect correlation" with the seawater surface temperature.

Subsequently, paragraph IV shows that after applying the correction aimed at the secondary minima, the TSI explains 93% of the variance in the seawater surface temperature for the period up to and including the 1980s. And then paragraph V describes that the corrected TSI combined with the size of the hole in the ozone layer at the South Pole explains as much as 96% of the variance over the entire period since the last decade of the 19th century.

It is important to be aware that these results are based on values over a 3-year period. When the solar sensitivity for the average values over 3 years for the entire period is calculated combined with the size of the hole in the ozone layer, a value is found of 1,23 °C per W/m2 (explained variance: 96%).

However, when the solar sensitivity is calculated on the basis of the individual years up to and including the 1980s, a value of just 1,07 °C per W/m2 is found for the solar sensitivity (accompagnied with an explained variance of 63%). And a calculation of the solar sensitivity based on the individual years combined with the size of the hole in the ozone layer results in a value of 0,96 C per W/m2 (accompagnied with an explained variance of 84%). This induces the impression that in the perspective of individual years 'climate noise' plays a role in masking the sun's sensitivity, for example via phase differences.

The value found for solar sensitivity therefore depends strongly on the chosen calculation method. Since the highest explained variance (96%) is found for the solar sensitivity of 1,23 °C per W/m2 (based on the 3-year average over the entire period via the combination of the sun and ozone), this value is chosen in order to estimate the warming caused by the sun since the Maunder minimum at the end of the 17th century.
In the meantime, the TSI has increased from a value of 1360.274 W/m2 during the minima during the last 4 decades of the 17th century to a value of 1361,215 W/m2 during the most recent primary minimum year 2017. This corresponds to an increase of 0,941 W/m2 over a period of approximately 330 years.

This increase of 0,941 W/m2, combined with a solar sensitivity of 1,23 °C per W/m2, results in a temperature increase of 1,157 °C in 330 years. This corresponds to an average temperature rise of more than 0,35 °C per century; however, for the most recent period the average value is 2x larger, for: after the 3-year minimum around the year 1912 the sun explains more than 0,7 °C of the warming during the past 110 years (of which 0,38 °C for the 3-year minima between 1912 and 1996 involving a period of 84 years = by average 0,45 °C per 100 year).

* The February article refers to Zharkova et al. (June 24, 2019)²⁴ who associate their research based on various magnetic properties of the sun, a parallel with the work of Akasofu (2010) where a natural impact trend of by average 0,5 °C for the 20th century is described. On March 4, 2020, Zharkova's publication has been withdrawn by the journal Nature despite objections made by 3 of the 4 authors (this action was taken under pressure of arguments primarily related to an assumption made regarding the existence of uncorrelated fluctuations in the movement of sun and Earth around the barycenter; the magnitude and direction of these fluctuations is disputed by peer reviewers, who assume that the motion of sun and Earth are each under the same influence of the planet Jupiter + some other planets).

VII - Pre-satellite era: other data sets show the same profile around primary minima

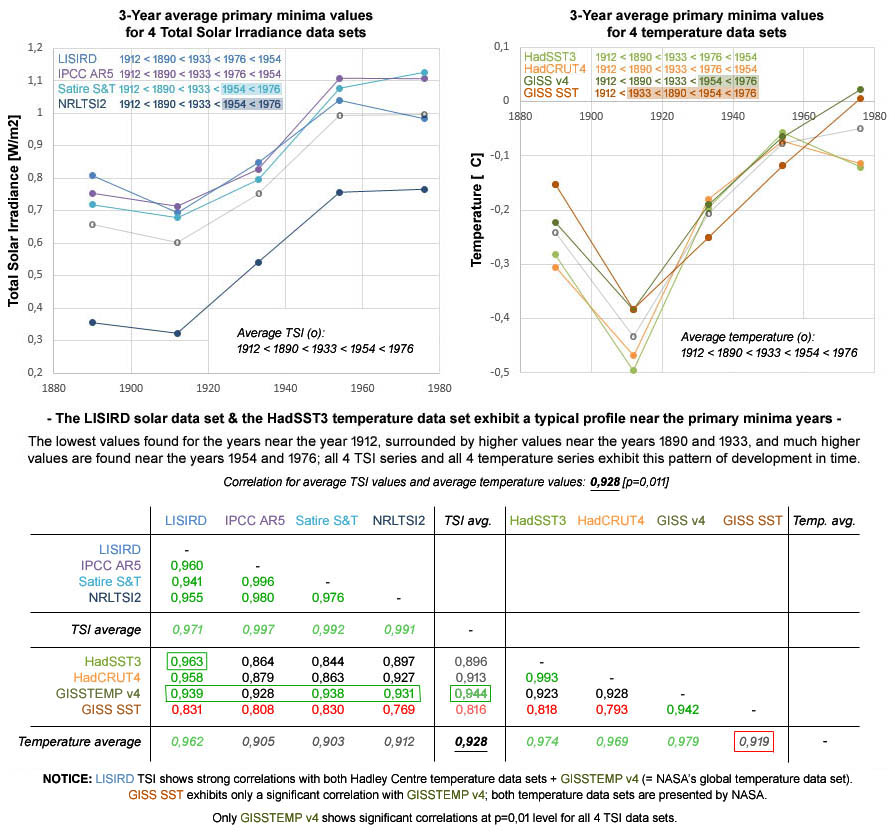
The previous paragraphs describe that the LISIRD TSI data set shows for the years near the minima a particularly strong parallel with the HadSST3 data set for seawater surface temperature. This paragraph places the combination of both data sets in a broader perspective through a comparison between values based on the 3-year primary minima for the pre-satellite era. A total of 4 TSI data sets (LISIRD, IPCC AR5, Satire S&T and NRLTSI2) and 4 temperature data sets (HadSST3, HadCRUT4, GISSTEMP v4 and GISS SST) are used in this comparison. Only the HadSST3 data set and GISS SST data set involve seawater surface temperature.

Figure 11 shows that all 8 data sets show approximately the same profile for the primary minimum years in the pre-satellite era. The 3-year period near 1912 describe the lowest value in every data set; 1890 and 1933 show higher values and 1954 and 1976 show even higher values. It is also striking that the average values of the 4 TSI data sets and the average values of the 4 temperature data sets produces a correlation of 0,928 [p=0,011].

Figure 11: A comparison between 4 TSI data sets (LISIRD, IPCC AR5, Satire S&T and NRLTSI2) and 4 temperature data sets (HadSST3, HadCRUT4, GISSTEMP v4 and GISS SST) reveals the same pattern for all data sets involving the primary minima in the pre- satellite era. All data sets produce the lowest value for the 3-year period near 1912; 1890 and 1933 show higher values and the highest values are found for 1954 and 1976.

Figure 11 also describes that the internal consistency between the 4 TSI data sets is slightly higher in comparison to the 4 temperature data sets. This can partly be explained by the fact that 2 of the temperature data sets relate to the temperature of the seawater surface (HadSST3 and GISS SST) and the 2 other temperature data sets relate to the global temperature (HadCRUT4 and GISSTEMP v4). However, it is also noteworthy that the GISS SST temperature data set from NASA in particular describes a relatively large deviation from the other data sets. This implies that the GISS SST is far less consistent with the other 6 data sets than the GISSTEMPv4, while the other seawater surface data set HadSST3 shows a much higher consistency with the other data sets.

Also, the correlation between the GISS SST and GISSTEMP v4 shows a value of 0,942, which is also clearly less consistent compared to the 0,993 correlation between the HadSST3 and the HadCRUT4 data sets. In short, the Hadley Center data sets are clearly more consistent with each other than the two NASA data sets.

Curiously, the GISSTEMP v4 data set shows with 3 of the 4 TSI data sets in figure 11 a correlation with a value barely lower than the value of the correlation with the associated GISS SST data set. From a comparison between all 8 data sets can be concluded from these observations that the GISS SST data set by far shows the greatest deviation. Also striking, the difference between the GISS SST and the two temperature data sets of the Hadley Center (HadCRUT4 and HadSST3) is clearly larger than the mutual differences between various TSI and temperature data sets.

This implies that the profile of the TSI data sets and the temperature data sets are not easily distinguishable from each other. The internal consistency between various combinations of TSI and temperature data sets appears to be even greater than between the two temperature data sets of the Hadley Center and NASA - whereby again the GISS SST in particular manifests as a data set with a strikingly large deviation from the other data sets.

Relevant as well, the LISIRD shows with 6 out of the 7 other data sets a correlation that is higher than the correlation between the average values for the 4 TSI data sets and the average values for the 4 temperature data sets. The GISS SST is the only exception here as well. And it is also striking that the correlation between LISIRD TSI and the average values of the 4 temperature data sets (0,962) is higher than the correlation between the GISS SST and the average values of the 4 temperature data sets (0,919).
The overall picture shows that, in contrast to the exceptional position of the GISS SST data set, the corresponding GISSTEMP v4 data set for the global temperature shows relatively strong correlations with the four TSI data sets (where the correlation values consistently have the p=0,01 significance level). In short, the two global temperature data sets collectively show a stronger pattern of correlations with the TSI data sets than the average of the two seawater surface temperature data sets.

The profile that is described to be present in all 8 data sets can be specified further for the 4 temperature data sets. The overview below shows very small temperature differences between especially the periods around 1912 and 1976 (these two periods involve the most recent bottom phases of the multi-decadal cycle, as described in the August 2019 article). The differences are within a bandwidth of just 0,022 °C. This means that the 4 temperature data sets show more or less the same temperature increase between the two 3-year periods around the years 1912 and 1976. This implies that there is a high consensus found for the size of the temperature rise in the period between those 2 minima; this involves both seawater surface temperature data sets and both global temperature data sets.

1890 (= 1889-1891): HadSST3 +0,215 °C; HadCRUT4 +0,163 °C; GISSTEMP v4 +0,160 °C; GISS SST +0,230 °C;
1912 (= 1911-1913): HadSST3 +0,0 °C; HadCRUT4 +0,0 °C; GISSTEMP v4 +0,0 °C; GISS SST +0,0 °C;
1933 (= 1934-1935): HadSST3 +0,298 °C; HadCRUT4 +0,288 °C; GISSTEMP v4 +0,193 °C; GISS SST +0,133 °C;
1954 (= 1953-1955): HadSST3 +0,440 °C; HadCRUT4 +0,394 °C; GISSTEMP v4 +0,320 °C; GISS SST +0,266 °C;
1976 (= 1975-1977): HadSST3 +0,374 °C; HadCRUT4 +0,354 °C; GISSTEMP v4 +0,360 °C; GISS SST +0,376 °C;
1996 (= 1953-1955): HadSST3 +0,711 °C; HadCRUT4 +0,767 °C; GISSTEMP v4 +0,800 °C; GISS SST +0,683 °C;
2017 (= 2016-2018): HadSST3 +1,029 °C; HadCRUT4 +1,158 °C; GISSTEMP v4 +1,316 °C; GISS SST +1,035 °C.

In the final paragraph (X Discussion & conclusion) is calculated that the warming between the 17th century (when the Maunder minimum occured) and the 3-year period around the year 1912 amounts to approximately 0,5 °C based on the solar sensitivity. This implies that seawater surface temperature has increased by 1,5 °C in total since the 17th century; for the atmosphere the value is 0,15-0,30 °C higher with a value of 1,65-1,80 °C.

Finally, the percentage increase between the 3-year periods around 1996 and 2017 relative to the increase between the 3-year periods around 1976 and 1996 shows a remarkable difference. Because the two data sets from the Hadley Center show a slight delay in the temperature rise, while the two data sets from NASA show a relatively large acceleration.

Overview of the percentage differences during the last 2 solar cycles:

- data sets Hadley Centre: HadSST3 -5,6%; HadCRUT4 -5,3%;
- data sets NASA: GISSTEMP v4 +17,3%; GISS SST +14,7%.

These percentage differences describe a fundamental inconsistency between the two data sets of the Hadley Center and the two data sets of NASA.

VIII - Satellite era: ACRIM-PMOD controversy crucial to impact of the sun

Paragraph VI of the February article describes a controversy over the influence of the sun that started in the 1990s. Two of the three research teams responsible for all facets of TSI satellite measurements since the beginning of satellite measurements in 1978, have publicly distanced themselves from the PMOD method which is part of the IPCC vision in AR5^25-27.

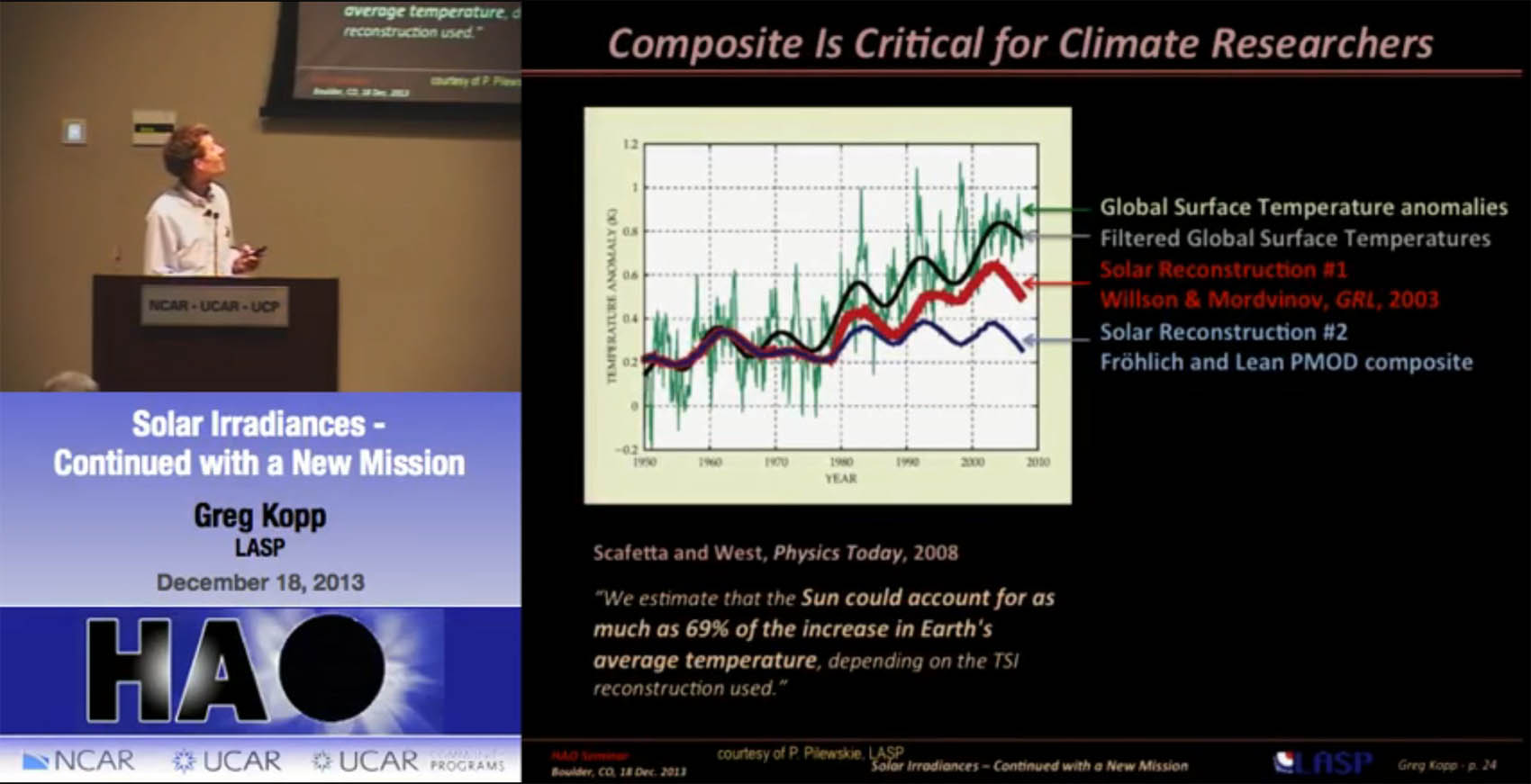
This is a crucial issue, for, figure 8.10 in AR5 ⁹ (= figure 12, see illustration) shows that only the PMOD describes TSI minima to have a negative trend, while both the ACRIM, RIMB and SORCE/TIM describe a positive trend for the minima starting from the 1980s - especially when the 22-year magnetic solar cycle is taken into account. The Belgian RIMB describes a continuous increase from the minimum of the mid- 1980s similar to the LISIRD TSI data set.

The IPCC does recognize in AR5 that for studying long-term changes in the activity of the sun, attention is usually focused on the minima because they are a more "stable" and a more "relevant" indicator for the long-term trend compared to the maxima⁹ However, the IPCC then uses the following reasoning to completely ignore the significance of the minima:

"To avoid trends caused by comparing different portions of the solar cycle, we analyze TSI changes using multi-year running means."⁹

It is also important that the IPCC in its descriptions frequently refers to the 11-year solar cycle; however, the 22-year magnetic solar cycle is never being mentioned. In the report of the "expert review comments" accompanying the IPCC AR5 report (2013), one expert reviewer referred to the 22-year cycle in passing, but in the IPCC response the phenomenon is not mentioned²⁸.

In addition to the IPCC's choice not to take into account in its analysis that the minima in particular are indicative of the long-term trend of total solar irradiance, the missing of the 22-year magnetic solar cycle is another fundamental shortcoming is the IPCC framework. For, only the 22-year cycle can serve to identify the relative importance of the primary minima, which is also important for the impact of 'climate noise' due to for example the relatively large fluctuations in the UV spectrum of the sun (these fluctuations can be at the order of 100x larger than the fluctuations within the entire spectrum²⁹). This point is also relevant for studying the temperature impact of the ozone depletion, which is known to play a crucial role in blocking UV rays that are harmful to humans.

In paragraph VII of the February article a detailed description is presented for the LISIRD data set. Though the LISIRD is not an "official" TSI, in the view of LASP's principal investigator Greg Kopp (figure 13) it does present the best values available to the experts; the satellite era data is based on the Community-Consensus TSI Composite³⁰.

Figure 13: LISIRD author Greg Kopp describes the controversy among TSI experts about the impact of the sun in climate change.

IX - Physical substantiation for impact of sun is conceptually more simple than CO2 hypothesis

This paragraph presents a description of the physical mechanisms for the sun (IX-a) and CO2 (IX-b) in the climate system.

• IX-a The physical mechanism behind the influence of the sun on the climate

The sun is known as the driving force behind all climate and weather phenomena. The mechanism is basically easy to understand: Earth surface temperature follows the total solar irradiance during the phase where the primary minima become manifest in the perspective of the 22-year magnetic solar cycle. The 22-year solar cycle arises from a complex of short and long-term cycles (all are based on magnetic activity) which determines both the amount & composition of solar radiation that reaches planet Earth's atmosphere.

The phase of the primary minima is the most stable and reliable indicator of long term solar activity. The minima arise when the pressure component in the energy waves of the sun is accompanied by a lower frequency³¹, combined with: a higher amplitude + a greater number of active regions³². It is also known that the composition of solar radiation shows large fluctuations, especially at the maxima; this is even accompanied by the formation of two maxima which are spread over submit a period of 2-3 years. The first maximum is characterized by, among other things, a high level of the far UV + many small sunspots & solar flares; the second maximum is characterized by large sunspots as well as large solar flares and auroras.

This explains why 'climate noise' arises relatively easily during maxima; Earth's atmosphere can more easily reflect (through for example Albedo) or absorb (through for example degradation of UV radiation in the ozone layer) the less powerful high-frequency solar energy. The December article describes that the correlation between TSI and temperature is for years near solar minima up to 4x higher than for years near solar maxima.

The correction for the secondary minima is justified on the basis of the magnetism: The switch of the magnetic poles of the sun occurs during the maxima of both the TSI and the sunspot cycle. And the magnetic field of the solar poles reaches the highest value during the TSI minima. In addition, TSI minima are on average accompanied by lower temperature values than the temperatures during the TSI maxima. This implies that the phase that is featured with a strong magnetic field at the solar poles is associated with both a low TSI and a relatively low temperature on Earth. In the perspective of a comparison between minima and maxima, the TSI is more dominant than the magnetic field of the solar poles.
When comparing the primary and secondary TSI minima, on the other hand, an opposite dynamic is found: the magnetic field becomes dominant with regard to temperature. Also, the temperature is structurally higher during the secondary TSI minima than is the case with the primary TSI minima. The WSO measurements for the magnetic field (see figure B1 in the December article) shows that the magnetic field of the solar poles during the secondary TSI minima usually also reached relatively high values relative to the directly surrounding primary TSI minima.
This shows that at the minima the magnetic field becomes more dominant for temperature development; this can be understood easily because the influence of the TSI during the minima is relatively small but the magnetic field is relatively large. Result: a greater magnetic flux is generated, which is accompanied by a higher impact from solar wind. The correction of the secondary dynamics neutralizes the impact of this inverse dynamic; this can be justified on the basis of both the phase differences and the opposite dynamics visible in the data. In numbers, an estimate can also be made with regard to the temperature sensitivity due to the magnetic field of the solar poles, which involves a value of about 0,5 °C per Gauss based on the perspective of the WSO measurements. In climate science, the magnetic field of the solar poles is not (yet) taken into account, nor is the phase difference with the TSI taken into account.

UV solar radiation is the primary source of energy for the atmosphere and it plays a central role in both the vertical, thermal and electronic structure of the atmosphere. It should be noted here that the UV spectrum forms 8% of the total solar spectrum at the top of the atmosphere, but only 3-5% at the surface of planet Earth. In addition, UV radiation plays a crucial role in the ozone cycle of the atmosphere. This is also important because ozone generates heat in the stratosphere through absorption of the sun's ultraviolet radiation in the higher atmosphere (stratosphere) and by absorbing rising infrared radiation from the lower atmosphere (troposphere).

The sun generates every day about 12% of all ozone in the atmosphere via UV radiation; the damage to the ozone layer ensures that more of the high-energy UV-C and UV-B radiation in particular can penetrate deeper into the atmosphere. Of the 3 possible factors (UV, cosmic rays and/or solar wind) that can play a role in the creation of the reinforcing factor, represents UV a candidate that can potentially have large effects in the circulation of the atmosphere. However, circulation models suggest that the variations are relatively small. Nevertheless, the cooling of the stratosphere that has arisen since the early 1980s logically indicates vertical transport of energy from the higher atmosphere to the lower atmosphere, in which UV plays a key role.

Both the December article and the February article describe patterns which show that the sun also has a clear 'footprint' in the ENSO cycle.

The scientific literature describes the temperature difference between a passive and active sun to be in the order of 1 °C on the basis of holes in Earth's crust or ice caps³³; Svensmark describes a slightly higher value for this: 1-2 °C ³⁴. These values are close to the estimate of 1,1 °C warming caused by the sun since the Maunder minimum (see section VI). But this requires a high reinforcing factor because the fluctuations in the TSI are relatively small in terms of the energy involved. However, the sun's energy is not just the photons measured through the TSI, because the energy of the sun also reaches Earth through magnetism and energetic particles. Both the impact on the climate and the associated physical mechanism of these 2 additional factors are not included in the view of the IPCC. It became clear in 2019 that for example the power of the magnetic field of the sun has been underestimated until very recently with a factor 10.

The recent extreme solar conditions also manifest in number of sunspots. In 2004 scientists working at the Max Planck institute determined that the number of sunspots in the 2nd half of the 20th century has reached a record level within the perspective of the past 8,000 years³⁵. However, in 2008 the basic value for the TSI was lowered from 1365 W/m2 to 1361 W/m2. Adjustments were subsequently made in 2015 as well with regard to the sunspots; as a result, the exceptional sun conditions of recent decades attract less attention.The video presentation by Prof. dr. Nir Shaviv below describes the continuing influence of the sun on climate in the perspective of the history of the Earth.

VIDEO: DTU lecture by Prof. dr. Nir Shaviv on the continuing role of the sun in climate change;
starting from 13:30 the video also discusses the perspective shown in figure 14 below.

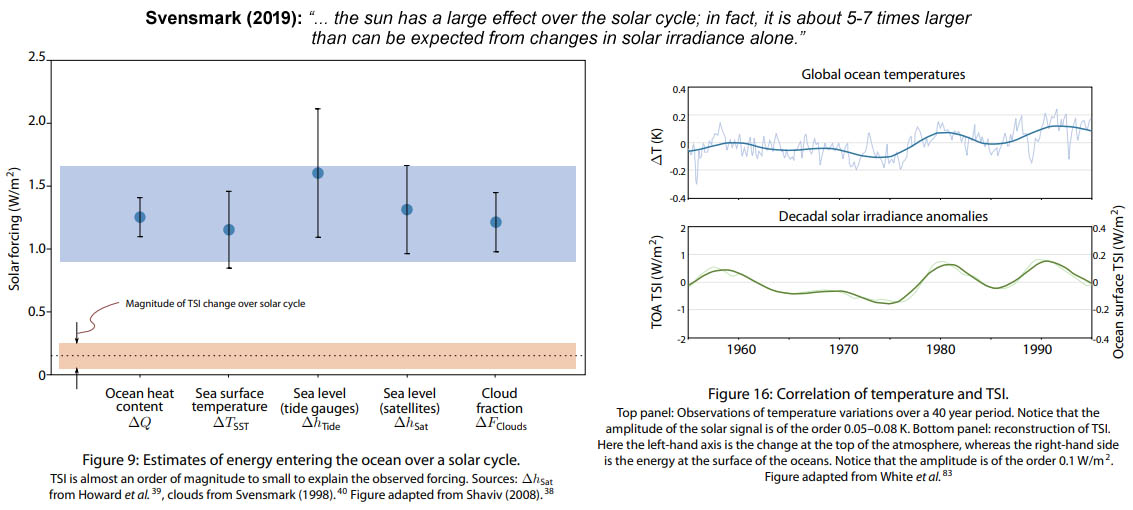
Figure 14: The sun has a large temperature impact during the 11-year solar cycle; the impact is 5-7 times larger than expected based on total solar irradiance (TSI) only³⁴.

TSI SHOWS THE DIRECT PART OF THE ENERGY OF THE SUN ONLY

At first glance the explanation for the influence of the sun may seem relatively simple; however, especially the aspect of the necessary reinforcing factor concerns a complex matter in terms of the numbers involved. One should be aware that the solar radiation measured at the top of the atmosphere only partly reaches and warms Earth's surface. Taking into account the spherical shape of Earth + an albedo factor of 30-39% (percentages according to Wikipedia), per square meters only about 15,25-17,5% of TSI reaches Earth's surface. Svensmark describes for the solar signal force in the ocean system involving the 11-year sunspot cycle a value of 0,2 W/m2³⁴ (see figure 14).
In terms of the energy the presence of a reinforcement mechanism is necessary. Experts in this specific matter assume that for the natural mechanism involved with the amplification of the solar signal there are 3 potential candidates: UV, cosmic rays and/or solar wind. Svensmark and Shaviv describe an (indirect) amplification factor for the 11-year solar cycle signal in the ocean system with an impact in the order of 5 to 7 times larger than the TSI signal itself^34,36. The description of Svensmark (see 'figure 16' in figure 14) implies that the 11-year solar cycle TSI amplitude of 0,5 W/m2 (= 5x the value of 0,1 W/m2 at Earth's surface) at the top the atmosphere (TOA) produces a temperature amplitude of 0,05-0,08 °C.
Svensmark's descriptions imply an impact of only 0,50-0,80 °C per W/m2 at Earth's surface; however, the solar sensitivity described in section III and section IV for the minima corresponds to a value of 6,0 °C per W/m2 at Earth's surface (after using the same multiplication factor of 5x used by Svensmark combined with the value: 1,2 °C per W/m2). This means that the long-term perspective of the minima in temperature development requires a reinforcing factor of 7,5x to 12x on top of the perspective of the solar cycle; this corresponds to an amplification factor of in total 37,5x to 84x compared to the TSI signal in the ocean system at Earth's surface (using the amplification value of 5 to 7 described by Svensmark).
The magnitude of these numbers can be understood via the fact that fluctuations for the TSI as a whole are relatively small with a variation of the order of 0,1%; however, the magnitude of the fluctuations varies greatly. For example: the UV spectrum variation is at the order of 10-20% of total TSI - which is approximately a factor of 100-200 higher compared to the entire solar spectrum²⁹. Svensmark describes that the fluctuations at a wavelength of 120-121 nm are accompanied by changes of the order of 40%, which is 400x higher than the fluctuations of the entire TSI spectrum³⁴. Extremely ultraviolet [EUV] frequencies show variations that can be as high as 6%, which equals to a factor of 30x higher than the 0,02% that applies to visible light. It is also important that EUV radiation consists of high-energy photons, which can have a large impact on the atmosphere.
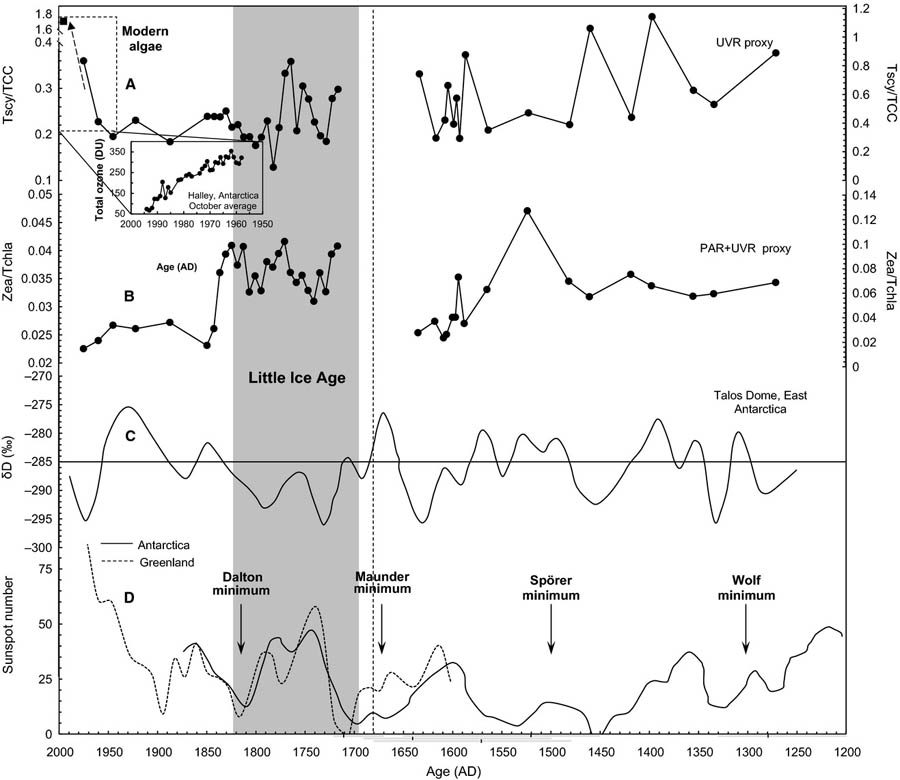
UV proxies based on algae show that in Antarctica the amount of UV radiation at the end of the 20th century increased by about 50% compared to the previous peaks with values of less than 1.2 Tscy/TCC that have occured halfway the previous millennium. This results in a hockey stick graph that is even steeper than is the case with the sunspots with values of almost 1.8 Tscy/TCC³⁷ (see figure 15).

In short, the dynamics due to the influence of the sun are clearly visible, but numerically the mechanism is not understood. This is probably because the energy of the sun arises from a combination of a direct influence of: (1) photons [UV], combined with indirect influences of: (2) energetic particles [solar wind] and (3) magnetic fields [cosmic rays].
The TSI measures only the direct influence of photons. However, the fluctuations of the sun are based on magnetism; this shows instantly that the impact of solar magnetism (combined with the influence of cosmic rays) can logically be at least as large in the perspective of dynamics that result from cosmic constellations. The following quotation from the work of van Geel & Ziegler ³⁸ provides an illustrative indication for this influence:

"Measurements show that between 1964 and the 1990s the total magnetic flux leaving the Sun (solar wind) increased by a factor of 1.4 with surrogate measurements indicating that it increased since the Little Ice Age by 350%, while the GCR flux decreased by about 50% to reach a low in the 1990s."

Figure 15: UV proxies based on scytonemine pigment formed by bacteria in algae in Antarctica (top part) show very high levels at the end of the 20th century (~1,8 Tscy/TCC), which results in a likewise 'hockey stick' shape graph that is also present for the perspective of the sun spots (bottom part); for the UV proxies the shape is even steeper for the sunspots³⁷. The regional decrease of ozone from 350 UD to 50 DU in the period 1960-2000 is shown in a separate box.

• IX-b The physical mechanism behind the influence of CO2 on the climate

Since the start of the industrial revolution, global CO2 concentration in the atmosphere has increased by about 50% from about 277 ppm around the year 1700 to values above 415 ppm in mid-April 2020. In a timespan of 320 years the amount of CO2 has increased from nearly 3 particles to over 4 particles per 10.000 particles in the atmosphere.

NASA describes the temperature impact of the total greenhouse effect to be 33 °C, including a cooling effect resulting from clouds of -5 °C³⁹. According the IPCC, the impact of clouds corresponds to a radiative forcing of -13 W/m2⁴⁰. According logics this implicates that all greenhouse gases together are responsible for a temperature effect of 38 °C (without the impact of clouds). The assumption is made that 9-26% of this temperature effect is generated by CO2; this implies an overall temperature effect for CO2 at the order of 3,42-9,88 °C (without considering a possible logarithmic effect that will depress the impact). A 50% increase in atmospheric CO2 should therefore logically result in a warming of 1,71-4,94 °C according this view. The IPCC hereby assumes that global warming since the beginning of the industrial revolution can be attributed largely to greenhouse gases. AR5 describes that it is thought that the temperature rise since the beginning of the industrial revolution may even be entirely due to greenhouse gases. It is argued that the greenhouse effect of CO2 is enhanced by feedback systems dominated by positive feedback; this also explains why the temperature impact of the increase in CO2 is higher than the 1,1 °C which has been found under laboratory conditions for a doubling of CO2. Since the 1990s the IPCC has been talking about a 'climate sensitivity' with a likely bandwidth of 1,5-4,5 °C, which refers to the temperature effect of a doubling of CO2.

However, this description is based almost entirely on a theoretical view. For, it was only in 2015 that direct empirical evidence was presented by researchers for the first time for the existence of the mechanism within the climate system described by the greenhouse theory²⁰. Those researchers have described in 2015 that CO2 has some influence (~10% of the trend) on the 'back radiation' of long wave (infrared) radiation from the atmosphere.

A fundamental problem in this view involves the fact that for every particle of CO2 in the atmosphere there are about 62,5 particles of the most dominant greenhouse gas available, namely: water vapor [H2O] (= ~2% for the first 15,5 miles; though there are other sources which describe 0,4% only for the full atmosphere). In other words, in addition to the 4 particles of CO2 per 10,000 particles in the atmosphere, there are approximately 200/250 particles of water vapor present in the climate system. In addition, approximately about the same amount of radiative forcing is attributed to 1 molecule of CO2 and 1 molecule of water vapor [H2O]. Logically, we can deduce from this that, in theory, water vapor can be held largely (possibly more than 98%) responsible for the greenhouse effect of 38 °C on the basis of the quantity compared to the other greenhouse gases. This perspective is confirmed by the magnitude of the temperature effect due to a doubling of CO2 under laboratory conditions, because the temperature rise of 1,1 C involved implies a contribution of less than 3% compared to the total greenhouse effect of 38 °C (without the impact of clouds). This percentage is also significantly lower than the CO2 contribution of 9-26% within the framework of the IPCC based on the greenhouse theory. The impact of CO2 compared to the other greenhouse gases (apart from the impact of water vapor) is estimated in AR5 at approximately 70%; for methane one thinks of a contribution of 4-9% and for ozone one thinks of a contribution of 3-7%. The latter percentages are representative of the so-called 'consensus'.

The view which attributes a lower impact for CO2 as a greenhouse gas on the basis of the quantitative ratios is consistent with among other things: Henry's law + the fact that CO2 follows temperature in the natural cycles and not the other way around. Henry's law describes that the increase of CO2 concentration in the atmosphere is partly due to the rise in temperature of the seawater surface. Based on expert judgements the rise in temperature accounts for about 15% of the rise in CO2 since the start of the industrial revolution. At a temperature rise of 1 degree Celsius, approximately 3% less CO2 can be dissolved in the ocean water surface. Fundamentally, this shows that a significant part of the rise in CO2 logically results from the rise in temperature and not the other way around. Moreover, the numerical analysis in this article shows that for the period up to and including the 1980s there is no room for a significant contribution of CO2, nor in the period after the 1980s; the contribution of ozone in the greenhouse effect (via the damage to the ozone layer) is indirectly considerably larger compared to CO2.

In short, both the perspective of the sun and CO2 show inconsistencies involving the magnitude of the ratios. For the sun this concerns mainly a reinforcing factor of 37,5 to 84; for the greenhouse theory the availability of an average of 62,5 particles of water vapor (or ~80% of this amount) compared to 1 particle of CO2 in the atmosphere represents a comparable ratio. Both factors are difficult to investigate empirically in the climate system. Especially because water vapor particles within the climate system manifest themselves in various states which each have a variable impact. The results under laboratory conditions for a doubling of CO2 indicate that the much greater availability of water vapor can potentially be bridged.
However, only the perspective of the CO2 theory includes fundamental inconsistencies which indicate that the impact of CO2 within the climate system is considerably more complex than what has been assumed under laboratory conditions. In addition, the climate system largely consists of negative feedback systems. The inconsistencies with regard to CO2 (involving Henry's law + the fact that CO2 is the temperature within the natural cycles) indicate that negative feedback systems are dominant inside the climate system, also with regard to the impact of CO2. Within the framework of the IPCC, it is assumed that positive feedback systems are responsible for an enhanced greenhouse effect. The PMOD-ACRIM controversy shows that the role of the sun became nihilized with arbitrary arguments. This is done on the basis of assumptions and adjustments that have been identified by several research teams at the highest level more than 2 decades ago; these very experienced researchers speak of a method that is not representative of what satellite data actually describe:

"Several TSI satellite composites have been proposed: ACRIM, PMOD, RMIB and those suggested by Scafetta and Dudok de Wit et al. Although these composites use different sets of TSI satellite records and merging methodologies, they are relatively equivalent since about 1992, the beginning of the ACRIM2 record, because they are all based on high-quality TSI observations. Yet, as clarified below, PMOD used their own modified versions of the original results compiled by the experiment teams for the SMM/ACRIM1, UARS/ACRIM2 and Nimbus7/ERB records to cover the period 1978-1992 and, therefore, its proposed record cannot be considered a real TSI satellite composite but a model construction. The ACRIM-PMOD controversy is about the scientific legitimacy of such modifications."⁴¹

X - Discussion & conclusion

This article demonstrates that 93% of the variance in seawater surface temperature [HadSST3] is explained by total solar irradiance [LISIRD], based on 3-year solar minima periods which cover the time span starting from the last decade of the 19th century up to and including the mid-1980s. This includes a correction aimed at the secondary minima. Also, for the entire period since the 1890 minimum, 96% of the variance is explained by the combination of total solar irradiance and decrease in ozone.

Also has been described that CO2, AOD and ENSO do not generate any significant value for the explained variance. This implies that the strong statistical relationship between CO2 and temperature represents a spurious relationship that is fully explained by the sun until the mid-1980s. During the transition between the 1985 and 1996 minima the emergence of the ozone problem has temporarily supported this sham relation. Ozone layer depletion due to the use of the artificial CFCs (not due to production of the by origin natural CO2) resulted in more UV solar radiation reaching Earth's surface. During the transition between the 1985 and 1996 minima the total solar irradiance shows a slight decrease, but subsequently it shows a continued rise between 1996 and 2008 and between 2008 and 2017.

The spurious relation between CO2 and temperature manifests itself in the perspective of both the primary and secondary minima, as well as in the combination of both minima series. Only the correlations between seawater surface temperature and total solar irradiance show a stable relationship for both the period prior to the ozone problem and the entire period since 1880. After a correction aimed at the 3-year average TSI secondary minima (+0,123 W/m2), the magnitude of the correlation between seawater surface temperature and TSI for both periods is higher than the correlation between seawater surface temperature and CO2.

The relation between TSI [TOA] and sea surface temperature shows a solar sensitivity of 1,2 °C per W/m2 (involving just the TSI values above 1360 W/m2) for the 3-year average at the primary minima (+ as well for the secondary minima after applying the correction). This relationship explains also the entire warming between the 3-year periods near the 1996 and 2017 minima. The solar sensitivity also implies that the sun can be taken responsible for approximately 1,1 °C of the warming that became manifest since the Maunder minimum at the end of The 17th century, based on an interim TSI increase of 0,941 W/m2 up to including the solar minimum year 2017.

Paragraph VI in the December article describes a temperature trend of +0,0316 °C per decade for the period 1810-1902 based on the PAGES 2k proxies. Since the year 1902 is a secondary minimum and the year 1810 is a primary minimum (with the succession of 2 primary minima in a row in the first decades of the 18th century taken into account), the correction should also be applied to the secondary minimum year 1802 in order to make a comparison with the PAGES 2k proxies. The 3-year TSI average around the years 1810 and 1902 yields an increase of 0,052 W/m2. Combining this value with the correction aimed at the secondary minima (+0.123 W/m2) this results in a total increase of +0,175 W/m2, which produces a value of +0,21 C via the solar sensitivity of 1,2 °C per W/m2. The calculated temperature difference based on the sun is therefore only about 0,1 °C smaller for the period 1810-1902 compared to the temperature trend found for the same period based on the PAGES 2k proxies.

A similar calculation has been made for the warming between the Maunder minimum and the 3-year period around the year 1810. The PAGES 2k proxies show a development with a slightly lower temperature near the Maunder minimum compared to the year 1810. The total solar irradiance suggests for the warming between the Maunder minimum and the 3-year period around the year 1810 a value of 0,40 °C; this results in a temperature increase of in total 0,61 °C for the period between the Maunder minimum and the 3-year period around 1902.
A control calculation involving the temperature difference between the Maunder minimum and the 3-year period around the primary minimum year 1912 (which has provided a stable reference point in paragraph VII compared to the period around 1976) yields a temperature rise of 0,51 °C. So, the results are consistent for the PAGES 2k proxies and the TSI; both methods produce a small temperature rise for both the 18th century and the 19th century. Combined with the overview presented in paragraph VI concerning the temperature development relative to 1912, one can deduce that the warming of the seawater surface temperature since the Maunder has been more than 1,5 °C. Meanwhile, the global temperature has risen about 0,15-0,30 °C faster than the seawater surface: the HadCRUT4 data set produces a value just over 1,65 °C and the GISSTEMPv4 data set produces a value just over 1,80 °C.

Because of phase differences between the sun and the ocean system (for example, the impact of ENSO is delayed with up to around 6 months) the data based on 3-year periods around the solar minima is likely more stable and a more reliable compared to data on based on the individual minimum years. Apparently, the impact of 'climate noise' has been reduced to a very low level. Also, the first 2 decades of the 21st century are characterized by low volcanism; therefore this might also explain a (small) part of the temperature rise since the 17th century; however, this involves likely not much more than a few hundredths of a degree Celsius.

Additionally, 55% of the HadSST3 warming between the 3-year periods near the 1976 and 2017 minima is explained by the sun, as shown in figure 10B. The ozone problem has ensured that more solar radiation has been able to reach Earth's surface; this largely explains the rest of the interim warming during this period.

Recently, several claims have been presented in the scientific literature by researchers who are using different research approaches in order to conclude that CFCs have had a temporary but nevertheless very significant impact in the development of the relatively rapid warming since the 1970s. In 2013 Prof. dr. Qing-Bin Lu of the University of Waterloo (Canada) claimed that CFCs combined with cosmic rays (under the influence of the sun's magnetic field) are the main cause of the warming since 1850⁴². Also, in January 2020 a group of researchers from the US, Canada and Switzerland reported that CFCs explain about 1/3 of the warming + about half of warming at the North Pole between 1955 and 2005⁴³. Since the year 2009, geophysicist Peter Langdon Ward has presented research centralizing the role of ozone in the climate.

With the use of 4 TSI data sets + 4 temperature data sets has been shown that all data sets show the same characteristic pattern at the 3-year average around the primary minima for the period 1890 to 1976. The lowest value within this pattern always manifests at the 3-year average near the 1912 minimum; the 1890 and 1933 minima show markedly higher values and the 1954 and 1976 minima show even higher values. Also relevant, the 4 TSI data sets do not clearly differ from the 4 temperature data sets; the variance within both groups of data sets is clearly greater than between the two data set groups. The two groups show a correlation with a value of 0,928 [p=0,000] based on the mean values.
For 2 out of 4 TSI data sets (LISIRD & IPCC AR5) as well as for both temperature data sets presented by the Hadley Center (HadSST3 and HadCRUT4), the 5 minimum values based on the 3-year average show exactly the same sequence. The most differentiating data set concerns the GISS SST data set.
Also striking, the perspective of the primary minima shows for both data sets of the Hadley Center a slight delay in the temperature development during the last two full solar cycles (1976-1996 and 1996-2017) while both NASA data sets show a relatively strong acceleration.
The highest correlation found in this perspective with a combination of a TSI data set and a temperature data set concerns the couple that is has produced the main results in this study, namely: the combination of the LISIRD and the HadSST3.

A description has been presented for the physical mechanism that explains the influence of the sun on the climate. The scientific literature presents detailed descriptions for three candidates (UV, cosmic rays and/or solar wind) involved with the emergence of the reinforcing mechanism necessary to explain the temperature effect found during the 11-year solar cycle. In this study it has become clear that an even greater reinforcing mechanism is active in the course of the minima between the 3-year periods around the 1890 and 2017 minima - which involves a period of 130 years in total.

This study has identified some crucial shortcomings in the IPCC's framework. On the one hand, these shortcomings explain how the alleged "not understood" link⁴⁴ between solar activity and Earth's climate has become manifest, and on the other hand these points provide tools serving for a better understanding of the relationship between sun & temperature

• 1 - The IPCC analysis does not take into account the 22-year magnetic solar cycle
• 2 - The IPCC analysis does not sufficiently take into account the significance of solar minima
• 3 - The IPCC analysis does not take into account the influence of the magnetic field of the sun (especially important for the minima)
• 4 - The IPCC analysis builds its conclusion regarding the sun on the PMOD data set, despite the fact that various TSI expert teams perceive the PMOD to be not representative for the satellite measurements
• 5 - The IPCC assumes the temperature effect of the 11-year sunspot cycle is only 0,06 °C (based on CMIP5 climate models); however, Wikipedia describes the impact to be 2-4 times higher, namely: 0,18 +/- 0,06 °C, based on Camp & Tung (2007)⁴⁵
• 6 - The IPCC does not take into account that within the natural cycles CO2 follows the temperature and not the other way around
• 7 - The IPCC does not take into account Henry's law (~ 15% of the CO2 rise is due to the temperature rise; this results in a theoretical inconsistency with the theory that CO2 is largely responsible for the temperature rise since 1850)
• 8 - With regard to long-term trends, the IPCC does not take into account the fundamental difference before and after the manifestation of the ozone problem (+ the emergence of the inverse relationship between temperature development in the lower and higher atmosphere)
• 9 - The IPCC puts too much emphasis on short-term trends: in the study of recent trends in global temperature, the influence of the multi-decadal natural cycle must be taken into account (globally this is mainly caused by the sun; cycles within the ocean system play a role locally).

These points show that the IPCC describes an incomplete unbalanced view with the role of the sun structurally being nihilized, combined with a tendency to attribute changes in the climate system to anthropogenic influences. Inconsistencies in the statistical relationship between temperature development and CO2 are structurally being ignored. Illustrative for this is the research showing that in the year 2015 researchers reported that they had found the first piece of empirical evidence for the existence of any influence of CO2 on the impact (just ~10% of the trend) of the radiation of the atmosphere based on data over a period of only 11 years²⁰.

The inverse relationship between temperature development in the lower atmosphere (troposphere) and the higher atmosphere (stratosphere) only started emerging in the early 1980s; this development coincides with the period in which the ozone layer became depleted. The IPCC assumes that CO2 can be held responsible for this. However, the IPCC does not make any demands with regard to consistent trends in its models for the periods before and after this inverse relationship has arisen. This study describes that the total solar irradiance around the minima shows consistent correlations with the temperature development for almost all periods starting from the year 1880, with exception to the transition between the minima around the years 1985 and 1996 - note: ozone level reached an absolute low in the year 1994. However, this does not imply that the strong relationship between sun and temperature is limited to the minima; for, there are several research approaches known that can demonstrate the strong relationship between sun and temperature⁴⁶.

Based on the analysis above, it may be concluded that the temperature development is largely determined by the sun combined with the antropogenic influence on the ozone layer. Based on the decrease of the impuls momentum in the movement of the sun around the barycenter (which correlates with the power of the sun), a temperature impact at the order of -0,1 °C for the coming 3 decades can be taken into account - in accordance with the description in the work of Scafetta described in the December article. In addition, based on the expected recovery of the ozone layer in the next 3 decades, the possibility of an impact at the order of -0,2 °C can also be taken into account. Logically, both effects can potentially lead to a temperature impact of in total -0,3 °C towards the year 2050. This is in line with the decrease of several hundredths of a degree Celsius described in the supplementary appendix in the article of June 2019 that can be foreseen based on an analysis focused on the multi-decadal climate cycle. That earlier estimate was made without being aware that the sun is largely in control of the climate cycle.

Quick summary: temperature follows the total solar irradiance (TSI) during the minima up to and including the mid-1980s; subsequently, ozone depletion disrupts this relationship, especially in the period between 1984-86 and 1995-97.

* A word of thanks to André Bijkerk for his editorial advices on the series of 5 articles (all devoted to the influence of natural cycles on the climate) presented since June 2019; André wrote several articles about the influence of the sun via cloud cover (this topic is also discussed in Prof. Shaviv's video presentation in section IX-a), see: HERE and HERE.

Figure A: solar flare arising from solar magnetic activity.

VIDEO: NASA description for the solar cycle.

The solar cycle is accompanied by a cosmic movement of the sun around the barycenter;
the mechanism is described by detail in the appendix of the December article.

hands

References:

1 - Artikel in Volkskrant: Warmt CO2 het klimaat echt wel op? (en nog drie knellende vragen die klimaatsceptici vaak stellen) [Article in Volkskrant: 'Does CO2 really heat up the climate? (and three more pressing questions climate skeptics often ask)'] (Feb 8, 2020).
2 - Artikel in Trouw: De zon is de meest nabije ster, maar we begrijpen er nog niet veel van [Trouw article: 'The Sun is the closest star, but we don't understand much yet] (Dec 15, 2019).
3 - The Sun and the Earth's Climate: Solar signals in surface climate - J.D. Haigh (October 2007).
4 - Met Office Hadley Centre observations datasets: HadSST3.1.1.0 Data [annual globe] (2019).
5 - LISIRD - Historical Total Solar Irradiance Reconstruction, Time Series (2018); author: Greg Kopp is lead researcher of SORCE/TIM project by LASP (biography).
6 - NASA: Stratospheric Aerosol Optical Thickness.
7 - Ensembloe Oceanic Nino Index (ENS ONI).
8 - Ozone Hole Area - NASA.
9 - IPCC, 2013: Climate Change 2013: The Physical Science Basis - 8 Anthropogenic and Natural Radiative Forcing - page 689 (chapter 8): "The year 1750, which is used as the preindustrial reference for estimating RF, corresponds to a maximum of the 11-year SC. Trend analysis are usually performed over the minima of the solar cycles that are more stable. ... Maxima to maxima RF give a higher estimate than minima to minima RF, but the latter is more relevant for changes in solar activity."
10 - 2018 Continues Record Global Ocean Warming - L. Cheng et al. (maart 2019) - Quote: "The vast majority of global warming heat ends up deposited in the world's oceans, and ocean heat content (OHC) change is one of the best - if not the best - metric for climate change (Cheng et al., 2019)".
11 - WMO: Key Climate Change Indicators from the Ocean (2017 update).
12 - Copernicus (EU): 'INSIGHTS INTO THE ROLE OF THE OCEANS IN THE EARTH ENERGY BUDGET' - K. von Schuckman (November 2017) - Citaat sheet 10: "The Earth energy imbalance can best be estimated from changes in ocean heat content, complemented by radiation measurements from space (von Schuckmann et al., 2016, NCC)".
13 - The unstable CO2 feedback cycle on ocean planets - D. Kitzmann et al. (August 2015).
14 - Greenhouse gas growth rates - J. Hansen & M. Sato (September 2004); source describes 14% for period 1850-2003, adjusted for 1850-2018 the percentage increases to 15%.
15 - Met Office Hadley Centre observations datasets: HadCRUT4 Data: download [global (NH+SH)/2] (2019)
16 - The Gnevyshev-Ohl Rule and Its Violations - N.V. Zolotova (February 2015).
17 - Gnevyshev-Ohl rule for strong solar proton events - M. Ogurtsov & M. Londholm (March 2016).
18 - The Gnevyshev-Ohl Rule for Physical Parameters of the Solar Magnetic Field: The 400-Year Interval - Yu.A. Nagovitsyn et. al. (October 2008).
19 - IPCC, 2013: Figure SPM.5
20 - Observational determination of surface radiative forcing by CO2 from 2000 to 2010 - D.R. Feldman, et al. (2015).
21 - Seasonal and Diurnal CO2 Patterns at Diekirch, LU 2003 - 2005 - F. Massen et al. (March 2007); section 4.1 & 4.3.
22 - Breakpoint lead-lag analysis of the last deglacial climate change and atmospheric CO2 concentration on global and hemispheric scales - Zhi Liu et al. (May 2018).
23 - Stratospheric ozone concentration - H. Ritchie & M. Roser (June 2018).
24 - Oscillations of the baseline of solar magnetic field and solar irradiance on a millennial timescale - V. Zharkova, et al. (June 2019).
25 - Astronomy and the Climate Crisis - A. Cooke (January 2012); pages 116-119.
26 - ACRIM3 and the Total Solar Irradiance database - R.C. Willson (February 2014).
27 - Modeling Quiet Solar Luminosity Variability from TSI Satellite Measurements and Proxy Models during 1980-2018 - N. Scafetta, et al. (November 2019).
28 - Expert Review Comments on the IPCC WGI AR5 First Order Draft -- Chapter 8 (2013) - comment 8-745.
29 - A solar irradiance climate data record - O. Coddington et al. (July 2016).
30 - Solar Irradiance Variability: Comparisons of Models and Measurements - O. Coddington et al. (December 2019); figure 6a.
31 - Background solar irradiance spectrum at high and low phases of the solar activity cycle - V. Ramió et al. (September 2002).
32 - Solar p modes in 10 years of the IRIS network - D. Salabert et al. (2004)
33 - The Role of the Solar Forcing in the 20th century climate change - N.J. Shaviv (2012)
34 - FORCE MAJEURE The Sun's Role in Climate Change - H. Svensmark (2019).
35 - Max Planck Institute: The Sun is more active now than over the last 8000 years (2004)
36 - Using the oceans as a calorimeter to quantify the solar radiative forcing - N. Shaviv (2008).
37 - An 800-year ultraviolet radiation record inferred from sedimentary pigments in the Ross Sea area, East Antarctica (July 2015)
38 - IPCC underestimate the sun's role in climate change - B. van Geel & P.A. Ziegler (2013)
39 - NASA - ISCCP: International Satellite Cloud Climatology Project (2008); quotation: "The net effect of clouds on the climate today is to cool the surface by about 5°C (9°F).".
40 - IPCC First Assessment Report.1990. UK: Cambridge University Press.table 3.1 (1990); quotation: "Clouds increase the global reflection of solar radiation from 15% to 30%, reducing the amount of solar radiation absorbed by the Earth by about 44 W/m². This cooling is offset somewhat by the greenhouse effect of clouds which reduces the outgoing longwave radiation by about 31 W/m². Thus the net cloud forcing of the radiation budget is a loss of about 13 W/m².".
41 - Modeling Quiet Solar Luminosity Variability from TSI Satellite Measurements and Proxy Models during 1980-2018 - N. Scafetta, et al. (November 2019).
42 - Cosmic-Ray-Driven Reaction and Greenhouse Effect of Halogenated Molecules: Culprits for Atmospheric Ozone Depletion and Global Climate Change - Q.-B. Lu (May 2013).
43 - Substantial twentieth-century Arctic warming caused by ozone-depleting substances - L.-M. Polvani et al. (January 2020).
44 - Klimaat brochure 'Klimaatverandering, Wetenschap en Debat' - Koninklijke Nederlandse Academie van Wetenschappen ['Climate change, Science & Debat' - Royal Dutch Academie of Sciences] (2011).
45 - Surface warming by the solar cycle as revealed by the composite mean difference projection - C.D. Camp & K. Kit Tung (July 2007).
46 - Re-evaluating the role of solar variability on Northern Hemisphere temperature trends since the 19th century - W. Soon et al. (August 2015).

CLIMATE INDEX:
• Millennium analysis: climate sensitivity CO2 is below IPCC bandwidth
• IPCC dataset sun explains half of warming since 1815
• Impact sun on climate is underestimated significantly
• Since 17th century: +1,1 °C by sun
• 1890-1976: Sun shows perfection correlation with temperature
• Side-role for CO2: solar activity explains warming since 1976
• Impact of CO2 on climate overestimated (substantially) due to 66-year cycle & El Nino

What do proxy climate indicators show?
• 2° Institute proxies: temperature rose in the past multiple decennia in a row even faster
• PAGES 2k Network illustration (2013)
• PAGES 2k Network illustration: 2019 hockeystick graphic vs 2013 temperature data

ClimateCycle articles in Dutch language:
• IPCC dataset zon verklaart met vulkanisme helft opwarming sinds 1815
• Tussen 1685 en 1976 volgde de temperatuur de totale zonnestraling
• Boekrecensie: SOLAR MAGNETIC VARIABILITY AND CLIMATE
• Online seminar door zonnefysicus Dr. Greg Kopp: 'Zonnestraling & klimaat'
• Impact zon op klimaat fors onderschat
• Sinds 17de eeuw: +1,1 °C door zon
• SAMENVATTING: Hoe ontstaat de Klimaatcyclus en wat is haar impact?
• 1890-1976: Zon toont perfecte correlatie met temperatuur
• Zon verklaart opwarming sinds 1976
• El Nino & 66-jarige cyclus: CO2 overschat
• 70-Jarige cyclus: opwarming overschat
• Global warming vs fluctuaties in 2 dagen
• Oceaan: diepzee koelt af
• KlimaatCyclus.nl